Calculs mathématiques d'emprunt bancaire
Comprendre les bases de calcul du financement des banques.
Calcul de la valeur acquise, la valeur actuelle en mathématiques financières
Dans cette vidéo, je vous présente les quatre formules les plus
utilisées en mathématiques financières. Ces formules dominent le monde
des calculs financiers.
La première de ces formules est la formule de l’actualisation d’un capital qui se trouve à une date dans le futur. Il faut savoir comme je l’ai déjà précisé que l’argent n’a pas la même valeur à des dates différentes, en finance c’est vérité absolue.
La deuxième formule est un peu la sœur de la première formule, consiste dans la détermination de la valeur d’un capital présent dans une période se situant dans le futur. Il s’agit dans ce cas de la formule de capitalisation.
La troisième formule est celle de la valeur acquise, il s’agit de la valeur d’une suite d’annuités au présent. Les annuités se situent à des dates dans le futur. Dans ce dernier cas, il s’agit simplement de l'actualisation de ces annuités, mais cela peut se calculer par une seule formule.
La quatrième formule est celle de la valeur future d’une suite d’annuités qui se situent. Dans le passé. Ces quatre formules dominent le monde de la finance, car tout calcul financier se réfère à l’une ou l’autre formule. Exemple pour calculer les mensualités d’un crédit, pour le rachat d’un crédit, pour évaluer la rentabilité d’un projet en comparant avec ce que rapporterait un placement d’argent....
À la fin de la vidéo, je vous donne deux exemples pratiques :
- le premier : il s’agit de répondre à la question "combien je dois placer aujourd'hui au taux de dix pour cent pour avoir vingt mille euros dans dix ans ? "
- La deuxième question : " je veux acheter un appartement qui coûte quatre-vingt mille euros dans dix ans, je veux savoir combien je dois placer chaque mois au taux d’un pour cent pour qu’au bout de dix ans je dispose de cette somme qui me permettra d’acheter l’appartement."
La première de ces formules est la formule de l’actualisation d’un capital qui se trouve à une date dans le futur. Il faut savoir comme je l’ai déjà précisé que l’argent n’a pas la même valeur à des dates différentes, en finance c’est vérité absolue.
La deuxième formule est un peu la sœur de la première formule, consiste dans la détermination de la valeur d’un capital présent dans une période se situant dans le futur. Il s’agit dans ce cas de la formule de capitalisation.
La troisième formule est celle de la valeur acquise, il s’agit de la valeur d’une suite d’annuités au présent. Les annuités se situent à des dates dans le futur. Dans ce dernier cas, il s’agit simplement de l'actualisation de ces annuités, mais cela peut se calculer par une seule formule.
La quatrième formule est celle de la valeur future d’une suite d’annuités qui se situent. Dans le passé. Ces quatre formules dominent le monde de la finance, car tout calcul financier se réfère à l’une ou l’autre formule. Exemple pour calculer les mensualités d’un crédit, pour le rachat d’un crédit, pour évaluer la rentabilité d’un projet en comparant avec ce que rapporterait un placement d’argent....
À la fin de la vidéo, je vous donne deux exemples pratiques :
- le premier : il s’agit de répondre à la question "combien je dois placer aujourd'hui au taux de dix pour cent pour avoir vingt mille euros dans dix ans ? "
- La deuxième question : " je veux acheter un appartement qui coûte quatre-vingt mille euros dans dix ans, je veux savoir combien je dois placer chaque mois au taux d’un pour cent pour qu’au bout de dix ans je dispose de cette somme qui me permettra d’acheter l’appartement."
L'importance des mathématiques financières
Quelques mots à propos des mathématiques financières pour commencer.
Sans aucun doute, tout le monde fait recours auxmathématiques pour faire des calculs de base dans la vie de tout les jours, que ce soit avec conscience ou pas. Pour un financier, cet outil est très précieuse est indispensable pour une bonne gestion des flux de l'argent.
L'un des intérêts desmathématiques dans la finance consiste à simplifier la complexité des calculs et problèmes financiers. Prenons un petit exemple pour en comprendre le sens :
Monsieur Y met 50000 Euro en banque au taux de 6%. On veut savoir combien il va avoir en banque la première année, la deuxième année, la troisième année,...
En procédant par des calculs spontanés :
Donc vous voyez que c'est très fatiguant de faire ces calculs, surtout si on veux savoir combien monsieur Y va avoir au bout de 10 ans ou 20 ans par exemple. Et bien c'est là que lesmathématiques financière vont intervenir pour simplifier tout calcul de ce genre.
On pourrait bien avoir une formule mathématique qui nous permet de calculer en une fois et à n'importe quelle date le montant du capital plus les intérêts générés.
Notant, en général, C0 est le montant du capital déposé à la date 0 (aujourd'hui) donc Cn et le montant du capital disponible à la banque au bout de la nième année et notons aussi i = le taux d'intérêt.
....
Donc il suffit de remplacer, dans cette dernière formule, n par le nombre d'années. Par exemple, au bout de la 20ième année, Monsieur Y va avoir en banque 50000(1+6%)20=160356,77 Euro.
Ce cas parait plus ou moins simple puisque on peut bien arriver à calculer, avec un peu de patience, ce que monsieur Y toucherait à la fin de la 20ième année. Mais si on se pose une question du type : comment peut on calculer, par exemple, la date à laquelle monsieur Y atteint 100000 Euro. mentalement, c'est impossible de faire le calcul, mais mathématiquement parlant, c'est très simple. Il suffit de résoudre l'équation Cn=C0(1+i)n à un seul inconnu n qui représente le nombre d'années écoulées sur le capital déposé à la banque. Ici on se demande à quelle date Cn=100000 donc en remplaçant dans la formule (Cn=C0(1+i)n) i par 6%, Cn par 100000 et C0 par 50000 on aurait :
100000=50000(1+0,06)n
==> 1,06n=100000/50000
==> 1,06n=2 Pour déterminer la valeur de n, il faut se servir d'une fonction qui s'appelle logarithme du signe "ln" (car l'une des caractéristiques de cette fonction et que lnXn=n.lnX)
==> ln1,06n=ln2
==> nxln1,06=ln2
==> n=ln2/ln1,06= 11.895660996576
C'est à dire que monsieur Y va avoir 100000 Euro en banque dans 11 ans, 0.895660996576x12m=10 mois et 0.747931958912x30j=22 Jours
Pour vérifier la réponse, il suffit de remplacer n par 11.895660996576 dans la formule 50000(1+0,06)n et voir si ça donne bien 100000 Euro.
Ce n'est qu'un simple exemple pour vous montrer à quel points est important de se servir des formulesmathématiques pour résoudre des problèmes pratiques.
Dans ce blog, je mettrais plus l'accent sur les calculs d'emprunt bancaire avec des explications et exemples pratiques.
Sans aucun doute, tout le monde fait recours aux
L'un des intérêts des
Monsieur Y met 50000 Euro en banque au taux de 6%. On veut savoir combien il va avoir en banque la première année, la deuxième année, la troisième année,...
En procédant par des calculs spontanés :
- Première année : Il va avoir les 50000 Euro plus les intérêts. Pour calculer les intérêts on multiplie le pourcentage d'intérêt 6% (c'est à dire 0,O6) par le montant déposé à la banque 50000 Euro, ce qui va faire : 50 000x0,06=3000 Euro. Donc en total, il va avoir à la fin de la première année : 50000 + 6%x50000 = 53000 Euro
- Deuxième année : Il va avoir les 53000 plus les intérêts calculés sur les 53000, c'est à dire : 53000 + 6%x53000 = 56180 Euro
- La troisième année : 56180 + 6%x56180 = 59550,8 Euro
Donc vous voyez que c'est très fatiguant de faire ces calculs, surtout si on veux savoir combien monsieur Y va avoir au bout de 10 ans ou 20 ans par exemple. Et bien c'est là que les
On pourrait bien avoir une formule mathématique qui nous permet de calculer en une fois et à n'importe quelle date le montant du capital plus les intérêts générés.
Notant, en général, C0 est le montant du capital déposé à la date 0 (aujourd'hui) donc Cn et le montant du capital disponible à la banque au bout de la nième année et notons aussi i = le taux d'intérêt.
- La première année on a : C1 = C0 + C0xi = C0(1+i)
- La deuxième année on a : C2 = C1 + C1xi = C1(1+i)=C0(1+i)(1+i)=C0(1+i)2
....
- Par déduction, la nième année on a : Cn=C0(1+i)n
Donc il suffit de remplacer, dans cette dernière formule, n par le nombre d'années. Par exemple, au bout de la 20ième année, Monsieur Y va avoir en banque 50000(1+6%)20=160356,77 Euro.
Ce cas parait plus ou moins simple puisque on peut bien arriver à calculer, avec un peu de patience, ce que monsieur Y toucherait à la fin de la 20ième année. Mais si on se pose une question du type : comment peut on calculer, par exemple, la date à laquelle monsieur Y atteint 100000 Euro. mentalement, c'est impossible de faire le calcul, mais mathématiquement parlant, c'est très simple. Il suffit de résoudre l'équation Cn=C0(1+i)n à un seul inconnu n qui représente le nombre d'années écoulées sur le capital déposé à la banque. Ici on se demande à quelle date Cn=100000 donc en remplaçant dans la formule (Cn=C0(1+i)n) i par 6%, Cn par 100000 et C0 par 50000 on aurait :
100000=50000(1+0,06)n
==> 1,06n=100000/50000
==> 1,06n=2 Pour déterminer la valeur de n, il faut se servir d'une fonction qui s'appelle logarithme du signe "ln" (car l'une des caractéristiques de cette fonction et que lnXn=n.lnX)
==> ln1,06n=ln2
==> nxln1,06=ln2
==> n=ln2/ln1,06= 11.895660996576
C'est à dire que monsieur Y va avoir 100000 Euro en banque dans 11 ans, 0.895660996576x12m=10 mois et 0.747931958912x30j=22 Jours
Pour vérifier la réponse, il suffit de remplacer n par 11.895660996576 dans la formule 50000(1+0,06)n et voir si ça donne bien 100000 Euro.
Ce n'est qu'un simple exemple pour vous montrer à quel points est important de se servir des formules
Dans ce blog, je mettrais plus l'accent sur les calculs d'emprunt bancaire avec des explications et exemples pratiques.
Calculer un emprunt : formules de base
Dans cette partie du blog, j'essaierai de simplifier la compréhension des mathématiques financières appliquées au différents calculs d'un emprunt ou d'un prêt. Je ne vais pas démontrer les formules que je vous expliquerai ici mais je me concentrerai plus sur leur signification et leur utilité dans la pratique de tous les jours pour éviter que cela ne soit un cours mathématique abstrait privé de tout sens pratique ou presque.
Dans les formules suivantes, vous avez l'essentiel des mathématiques financières, vous pouvez en déduire toutes les autres formules avec quelques simples touches mathématiques.
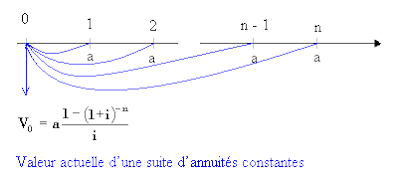 Valeur acquise Vn par un capital Vo placé pendant n périodes à un taux i
Valeur acquise Vn par un capital Vo placé pendant n périodes à un taux i

Actualisation / Capitalisation :

La première formule représente la valeur actuelle V0 (actualisation) d'une valeur future Vn actualisée sur n périodes à un taux i. De cette formule on en déduit la valeur future ou acquise Vn (capitalisation) en fonction du capital V0 placé pendant n périodes à un taux i.
Quelques exemple pratiques de ces formules :
1. Combien dois-je placer aujourd'hui au taux de 8% pour avoir 10 000 Euro dans 3 ans ?

2. Je veux acheter dans 5 ans une voiture au prix de 50 000 Euro, la banque me propose un taux d'intérêt de 12%. Combien dois-je placer mensuellement pour que je puisse disposer de ce montant exact dans 5 ans ?
Pour mieux répondre à cette question, il faut savoir traduire correctement ces données sur une ligne de temps et reposer la même question mais sous forme de schéma.
 Avec Vn= 50 000 Euro et n = 60
Avec Vn= 50 000 Euro et n = 60
Donc la question reformulée dans ce schéma est de savoir combien je dois placer mensuellement dès aujourd'hui pour que j'aie, grâce au produits de ces placements, au bout de la cinquième année, c'est à dire dans 60 mois, un montant de 50 000 Euro ?
Il faut bien savoir que le taux proposé par la banque est un taux annuel qu'il faut convertir au taux mensuel. Pour cela il faut distinguer entre un taux proportionnel et un taux équivalent.
Taux mensuel proportionnel = taux annuel /12 mois (les banques l'utilise incorrectement car ce taux équivaut au taux d'intérêts simples mais pas composés. En effet, le placement d'un Euro en intérêt simple mensuellement au taux i donnera à la fin de l'année un montant d'intérêt de 12i. De l'autre côté, le produit en intérêt de ce même placement pendant un an au taux annuel r donnerait un montant d'intérêt égal r. Donc, en supposant l'équivalence de ces deux montants d'intérêt nous obtiendront la formule du taux proportionnel )
Taux équivalent : c'est en fait le taux mensuel qui donnerait le même résultat que le taux annuel dans le cas d'un placement d'un même montant.
 Juste à titre d'information, au niveau des emprunts bancaires et surtout les emprunts immobiliers, on utilise le taux proportionnel et pas celui équivalent ce qui profite le plus aux banques puisque le taux proportionnel (1/12=1% dans notre exemple) est toujours plus grand que celui équivalent (0,95% dans notre cas) qui reflète le vrai taux mensuel correspondant au taux annuel proposé par la banque.
Juste à titre d'information, au niveau des emprunts bancaires et surtout les emprunts immobiliers, on utilise le taux proportionnel et pas celui équivalent ce qui profite le plus aux banques puisque le taux proportionnel (1/12=1% dans notre exemple) est toujours plus grand que celui équivalent (0,95% dans notre cas) qui reflète le vrai taux mensuel correspondant au taux annuel proposé par la banque.
Revenons à notre exemple, Il suffit donc de remplacer dans la formule Vn les valeurs suivantes : t=0,95%, n=60 et Vn= 50 000 pour trouver le montant a qu'il faut placer mensuellement pendant 5 ans.
 Donc si je place chaque mois un montant de 622,12 Euro au taux annuel de 12% j'aurais au bout de la cinquième année 50 000 Euro à raison de 37 327,2 Euro (= 622,12 x 60) remboursement des mensualités placées et le reste 12 672,8 Euro comme intérêts sur les placements.
Donc si je place chaque mois un montant de 622,12 Euro au taux annuel de 12% j'aurais au bout de la cinquième année 50 000 Euro à raison de 37 327,2 Euro (= 622,12 x 60) remboursement des mensualités placées et le reste 12 672,8 Euro comme intérêts sur les placements.
Plus de cas pratiques de calcul d'emprunts plus loin.
Réaction aux commentaires :
Pour répondre à votre question, on applique la formule de la valeur acquise cité ci-dessous comme illustré sur l'image suivante :
 Cette formule nous donne bien ce que j'aurais à la fin de la Xième année d'un placement de 1€ mensuellement au taux annuelle T%.
Cette formule nous donne bien ce que j'aurais à la fin de la Xième année d'un placement de 1€ mensuellement au taux annuelle T%.
Si je place 1€ chaque 3mois, je remplacerais T%/12 par T%/4 et 12.X par 4.X.
Dans les formules suivantes, vous avez l'essentiel des mathématiques financières, vous pouvez en déduire toutes les autres formules avec quelques simples touches mathématiques.
Valeur actuelle Vo d’une valeur future Vn actualisée sur n périodes à un taux i
 Valeur acquise Vn par un capital Vo placé pendant n périodes à un taux i
Valeur acquise Vn par un capital Vo placé pendant n périodes à un taux i
Actualisation / Capitalisation :

La première formule représente la valeur actuelle V0 (actualisation) d'une valeur future Vn actualisée sur n périodes à un taux i. De cette formule on en déduit la valeur future ou acquise Vn (capitalisation) en fonction du capital V0 placé pendant n périodes à un taux i.
Quelques exemple pratiques de ces formules :
1. Combien dois-je placer aujourd'hui au taux de 8% pour avoir 10 000 Euro dans 3 ans ?

2. Je veux acheter dans 5 ans une voiture au prix de 50 000 Euro, la banque me propose un taux d'intérêt de 12%. Combien dois-je placer mensuellement pour que je puisse disposer de ce montant exact dans 5 ans ?
Pour mieux répondre à cette question, il faut savoir traduire correctement ces données sur une ligne de temps et reposer la même question mais sous forme de schéma.
 Avec Vn= 50 000 Euro et n = 60
Avec Vn= 50 000 Euro et n = 60Donc la question reformulée dans ce schéma est de savoir combien je dois placer mensuellement dès aujourd'hui pour que j'aie, grâce au produits de ces placements, au bout de la cinquième année, c'est à dire dans 60 mois, un montant de 50 000 Euro ?
Il faut bien savoir que le taux proposé par la banque est un taux annuel qu'il faut convertir au taux mensuel. Pour cela il faut distinguer entre un taux proportionnel et un taux équivalent.
Taux mensuel proportionnel = taux annuel /12 mois (les banques l'utilise incorrectement car ce taux équivaut au taux d'intérêts simples mais pas composés. En effet, le placement d'un Euro en intérêt simple mensuellement au taux i donnera à la fin de l'année un montant d'intérêt de 12i. De l'autre côté, le produit en intérêt de ce même placement pendant un an au taux annuel r donnerait un montant d'intérêt égal r. Donc, en supposant l'équivalence de ces deux montants d'intérêt nous obtiendront la formule du taux proportionnel )
Taux équivalent : c'est en fait le taux mensuel qui donnerait le même résultat que le taux annuel dans le cas d'un placement d'un même montant.
 Juste à titre d'information, au niveau des emprunts bancaires et surtout les emprunts immobiliers, on utilise le taux proportionnel et pas celui équivalent ce qui profite le plus aux banques puisque le taux proportionnel (1/12=1% dans notre exemple) est toujours plus grand que celui équivalent (0,95% dans notre cas) qui reflète le vrai taux mensuel correspondant au taux annuel proposé par la banque.
Juste à titre d'information, au niveau des emprunts bancaires et surtout les emprunts immobiliers, on utilise le taux proportionnel et pas celui équivalent ce qui profite le plus aux banques puisque le taux proportionnel (1/12=1% dans notre exemple) est toujours plus grand que celui équivalent (0,95% dans notre cas) qui reflète le vrai taux mensuel correspondant au taux annuel proposé par la banque.Revenons à notre exemple, Il suffit donc de remplacer dans la formule Vn les valeurs suivantes : t=0,95%, n=60 et Vn= 50 000 pour trouver le montant a qu'il faut placer mensuellement pendant 5 ans.
 Donc si je place chaque mois un montant de 622,12 Euro au taux annuel de 12% j'aurais au bout de la cinquième année 50 000 Euro à raison de 37 327,2 Euro (= 622,12 x 60) remboursement des mensualités placées et le reste 12 672,8 Euro comme intérêts sur les placements.
Donc si je place chaque mois un montant de 622,12 Euro au taux annuel de 12% j'aurais au bout de la cinquième année 50 000 Euro à raison de 37 327,2 Euro (= 622,12 x 60) remboursement des mensualités placées et le reste 12 672,8 Euro comme intérêts sur les placements.Plus de cas pratiques de calcul d'emprunts plus loin.
Réaction aux commentaires :
Pour répondre à votre question, on applique la formule de la valeur acquise cité ci-dessous comme illustré sur l'image suivante :
 Cette formule nous donne bien ce que j'aurais à la fin de la Xième année d'un placement de 1€ mensuellement au taux annuelle T%.
Cette formule nous donne bien ce que j'aurais à la fin de la Xième année d'un placement de 1€ mensuellement au taux annuelle T%.Si je place 1€ chaque 3mois, je remplacerais T%/12 par T%/4 et 12.X par 4.X.
Emprunt immobilier : tableau d'amortissement financier
Un tableau d'amortissement des emprunts ou d'amortissement financier c'est un plan de remboursement d'un emprunt par le moyen de décaissements échelonnés. Il permet de mettre en évidence, à toutes les échéances, la part de l'emprunt remboursé, l'emprunt restant à rembourser, le montant de l'intérêt et la mensualité (intérêt+ emprunt remboursé). Ces quatre éléments sont primordiaux pour toute comparaison d'offre et la prise d'une meilleure décision.
Je mets à votre disposition : un tableau de calcul automatique des emprunts. Il vous permet de comparer facilement les différents offres sur le marché et de visualiser les différents éléments qui vous permettent de prendre votre décision d'emprunt.
Comment peut-on s'en servir ?
Je vous mets un exemple ci-dessous d'un emprunt de 5000 Euro au taux annuel de 12% à rembourser par 14 paiements mensuels. Une fois ces données introduites vous n'avez qu'à cliquer pour obtenir le tableau d'amortissement.

Dans le tableau vous aurez quatre colonnes principales que je vous explique ci-dessous en donnant comme exemple les calculs de la première ligne :
Réaction aux commentaires :

Le 1 dans la formule cité ici vient de la formule de la valeur actuelle d'une suite d'annuités (ou mensualités) qui devrait être égale au capital emprunté.
 Si vous remplacez V0 par K, a par m et i par t/12 vous arrivez à la même formule cité dans cette article, qui provient de l'actualisation de chaque montant "a" à la période 0.
Si vous remplacez V0 par K, a par m et i par t/12 vous arrivez à la même formule cité dans cette article, qui provient de l'actualisation de chaque montant "a" à la période 0.
Pour le calculer dans une calculatrice, oui c'est possible et il faut apprendre à le faire en une seule fois pour arriver au résultat le plus juste possible.
j'espère que cela répond à votre question.
Je mets à votre disposition : un tableau de calcul automatique des emprunts. Il vous permet de comparer facilement les différents offres sur le marché et de visualiser les différents éléments qui vous permettent de prendre votre décision d'emprunt.
Comment peut-on s'en servir ?
Je vous mets un exemple ci-dessous d'un emprunt de 5000 Euro au taux annuel de 12% à rembourser par 14 paiements mensuels. Une fois ces données introduites vous n'avez qu'à cliquer pour obtenir le tableau d'amortissement.

Dans le tableau vous aurez quatre colonnes principales que je vous explique ci-dessous en donnant comme exemple les calculs de la première ligne :
- Montant paiement : c'est la mensualité à payer = montant intérêt + part du capital à rembourser (principal). Pour la calculer, on a besoin d'une autre formule car la part du capital est inconnue pour le moment, donc pour la calculer nous avons une autre formule :
Cette formule est celle appliquée au niveau des emprunts immobiliers, pourtant elle n'est pas la seul méthode de calcul de la mensualité
- Montant intérêt : c'est la part d'intérêt = Restant à payer x taux mensuel proportionnel = 5000 x 12%/12 = 50
- Principal : La part du capital à rembourser = mensualité - montant intérêt = 384,51 - 50 = 334,51
- Restant à payer : C'est ce qui reste à payer en déduisant les parts du capital déjà payées = 5000 - 334,51 = 4665,49
Réaction aux commentaires :

- marie a dit…
-
bonjour sur votre exemple, pouvez-vous me dire à quoi correspond le chiffre 1 dans votre formule de calcul de la mensualité et peut-on faire cette formule sur une calculatrice;
merci
Le 1 dans la formule cité ici vient de la formule de la valeur actuelle d'une suite d'annuités (ou mensualités) qui devrait être égale au capital emprunté.
 Si vous remplacez V0 par K, a par m et i par t/12 vous arrivez à la même formule cité dans cette article, qui provient de l'actualisation de chaque montant "a" à la période 0.
Si vous remplacez V0 par K, a par m et i par t/12 vous arrivez à la même formule cité dans cette article, qui provient de l'actualisation de chaque montant "a" à la période 0.Pour le calculer dans une calculatrice, oui c'est possible et il faut apprendre à le faire en une seule fois pour arriver au résultat le plus juste possible.
j'espère que cela répond à votre question.
Emprunt bancaire : problèmes et solutions
Dans cette partie du blog, vous allez vous familiariser avec l'utilisation des formules mathématiques à la résolution de problèmes pratiques liés à la finance.
J'apprécierai tout problème ou question postée dans les commentaires, je m'efforcerai de lui apporter une bonne réponse. Alors n'hésitez pas.
3. Je veux emprunter 20 000 Euro à rembourser sur 5 ans pour financer un projet d'investissement. Pour cela, j'ai reçu deux offres de deux banques différentes :
Il faut noter qu'il n'y a pas qu'une solution possible pour des problèmes à résoudre au moyen desmathématiques financières .
Première solution :
On peut comparer les taux des deux banques. Mais attention, il faut comparer des choses comparables. Dans ce cas, les taux sont pour des périodes différentes. Pour cela, il faut calculer le taux équivalent de l'un par rapport à l'autre. C'est à dire, comparer, par exemple, au taux mensuel de 1%, le taux mensuel équivalent (à trouver) au taux de 3% (trimestriel)
Pour facilité la formulation du problème, on se demande, quelle est le taux d'intérêt mensuel i (inconnu) qui donnerais le même résultat que le taux trimestriel de 3% pour le placement d'un montant identique M pendant 3 mois (1 trimestre).
Donc pour supposer l'équivalence entre les deux résultats on a : Mx(1+i)4 = Mx(1+3%) c'est à dire que i = (1+3%)1/4 - 1 = 0,74% c'est ce taux mensuel équivalent au taux trimestriel de 3% qu'il faut comparer avec le Taux mensuel de 1% proposé par la banque A.
Donc vous voyez bien que la proposition de la banque B (0,74% mensuel) est moins coûteuse donc meilleure que celle de A (1% mensuel).
Deuxième solution :
On pourrait résoudre ce problème de la même façon mais en comparant, cette fois ci, le taux trimestriel de 3% avec le taux trimestriel équivalent au taux mensuel de 1%.
Le placement d'un montant M au taux de 1% mensuel pendant 3 mois : Mx(1+1%)4
Le placement du même montant M au taux t trimestriel pendant un trimestre (4mois) : Mx(1+t)
L'équivalence entre les deux taux d'intérêt donnerait le même résultat : Mx(1+1%)4 = Mx(1+t)
C'est à dire t = (1+1%)4 - 1 = 4,06 %
Donc vous voyez que vous arrivez au même résultat. Que vous utilisez la première solution ou la deuxième la proposition de la banque B reste la meilleure.
Troisième solution :
On pourrait résoudre ce problème en comparant tout simplement le montant d'intérêt de chacune des propositions et choisir la solution qui donnerait moins d'intérêts à payer. Pour cela, on calcule la capitalisation de 20 000 Euro pendant 5 ans pour les deux propositions.
20 000(1+0,01)60= 36 333,9 Euro. Ce qui donne un montant d'intérêt de 16 333,9 Euro (36 333,9-20 000)
20 000(1+0,03)3x5 = 31 159,3 Euro. C'est à dire un montant d'intérêt de 11 159,3 Euro
L'offre de la banque B donnerait moins d'intérêt à payer que l'offre de la banque A donc on préfère toujours un taux d'intérêt trimestriel de 3% qu'un taux mensuel de 1%.
4. Un couple vient d'avoir un bébé et ils se demandent comment ils peuvent lui offrir une meilleure éducation universitaire dans 18 ans plus tard. Pour cela il veulent savoir combien il faut placer annuellement, dès aujourd'hui, jusqu'à la 17ème anniversaire de leur fils pour avoir en retour, au bout de l'age de 18 ans et pendant quatre ans, quatre annuités de 20 000 Euro qui vont servir au financement de ses études universitaires.
La banque propose un TAEG de 10%.
Pour résoudre un tel problème, on peut toujours procéder de différentes façons et arriver nécessairement au même résultat. L'essentiel dans toutes ses solutions consiste à chercher un inconnu (le montant à placer annuellement dans cet exercice) en comparant des montants ramenés à une date précise dans le temps (toute comparaison en finance doit se faire à une même date en y capitalisant et actualisant des sommes dispersées dans le temps).
 En regardant le schéma, la question à poser est de dire que les différents montants à placer doivent être équivalents, financièrement parlant, aux mêmes montants que je vais recevoir de la banque dans 18 ans pendant 4 ans. Cette question nous donne bien l'équation à formuler pour trouver l'inconnu a mais il reste à choisir une date de comparaison (on peut choisir n'importe quelle date, la solution sera la même).
En regardant le schéma, la question à poser est de dire que les différents montants à placer doivent être équivalents, financièrement parlant, aux mêmes montants que je vais recevoir de la banque dans 18 ans pendant 4 ans. Cette question nous donne bien l'équation à formuler pour trouver l'inconnu a mais il reste à choisir une date de comparaison (on peut choisir n'importe quelle date, la solution sera la même).
Je vais choisir spontanément la date 0. Donc, on actualise les différents placements a à la date 0 pour obtenir une valeur actuelle des différents placements qui doit égaliser la valeur actuelle à la date 0 des différents montants à recevoir à partir de l'age de 18 ans.

D'où on a 9,20 a = 12 542,82 ==> a = 1 363,4 Euro, c'est à dire approximativement une moyenne de 114 Euro mensuellement.
5. L'utilisation de rachat ou regroupement de crédit dans la situation ou on est confronté à une série de mensualités de différents emprunts contractés pour financer des projets différents, est la meilleurs solution proposée par les banques jusqu'à présent. Pour en savoir plus cliquez sur la notion de rachat de crédit. Accédez aux liens ci-avant pour des exemples pratiques.
A suivre ...
Réaction aux commentaires :
Merci Laetitia pour votre commentaire. Effectivement j'ai eu une confusion en pensant au nombre de trimestres dans l'année au lieu du nombre de mois dans le trimestre.
Pour info utile :
Un semestre est une période de 6 mois [Le mot semestre vient du latin sex(six) et mentis(mois)] source : Wiktionnaire

Un quadrimestre est une période de 4 mois, une année se compose donc de 3 quadrimestres. Un trimestre est un espace de trois mois, il Y en a 4 sur l'année.
Un trimestre est un espace de trois mois, il Y en a 4 sur l'année.

J'apprécierai tout problème ou question postée dans les commentaires, je m'efforcerai de lui apporter une bonne réponse. Alors n'hésitez pas.
3. Je veux emprunter 20 000 Euro à rembourser sur 5 ans pour financer un projet d'investissement. Pour cela, j'ai reçu deux offres de deux banques différentes :
- Banque A : 1% (taux mensuel), remboursements mensuels
- Banque B : 3% par trimestre (taux trimestriel)
Il faut noter qu'il n'y a pas qu'une solution possible pour des problèmes à résoudre au moyen des
Première solution :
On peut comparer les taux des deux banques. Mais attention, il faut comparer des choses comparables. Dans ce cas, les taux sont pour des périodes différentes. Pour cela, il faut calculer le taux équivalent de l'un par rapport à l'autre. C'est à dire, comparer, par exemple, au taux mensuel de 1%, le taux mensuel équivalent (à trouver) au taux de 3% (trimestriel)
Pour facilité la formulation du problème, on se demande, quelle est le taux d'intérêt mensuel i (inconnu) qui donnerais le même résultat que le taux trimestriel de 3% pour le placement d'un montant identique M pendant 3 mois (1 trimestre).
- Le placement d'un montant M au taux mensuel i pendant 3 mois : Mx(1+i)4
- Le placement d'un montant M au taux trimestriel de 3% pendant 1 trimestre : Mx(1+3%)
Donc pour supposer l'équivalence entre les deux résultats on a : Mx(1+i)4 = Mx(1+3%) c'est à dire que i = (1+3%)1/4 - 1 = 0,74% c'est ce taux mensuel équivalent au taux trimestriel de 3% qu'il faut comparer avec le Taux mensuel de 1% proposé par la banque A.
Donc vous voyez bien que la proposition de la banque B (0,74% mensuel) est moins coûteuse donc meilleure que celle de A (1% mensuel).
Deuxième solution :
On pourrait résoudre ce problème de la même façon mais en comparant, cette fois ci, le taux trimestriel de 3% avec le taux trimestriel équivalent au taux mensuel de 1%.
Le placement d'un montant M au taux de 1% mensuel pendant 3 mois : Mx(1+1%)4
Le placement du même montant M au taux t trimestriel pendant un trimestre (4mois) : Mx(1+t)
L'équivalence entre les deux taux d'intérêt donnerait le même résultat : Mx(1+1%)4 = Mx(1+t)
C'est à dire t = (1+1%)4 - 1 = 4,06 %
Donc vous voyez que vous arrivez au même résultat. Que vous utilisez la première solution ou la deuxième la proposition de la banque B reste la meilleure.
Troisième solution :
On pourrait résoudre ce problème en comparant tout simplement le montant d'intérêt de chacune des propositions et choisir la solution qui donnerait moins d'intérêts à payer. Pour cela, on calcule la capitalisation de 20 000 Euro pendant 5 ans pour les deux propositions.
- Offre de la banque A :
20 000(1+0,01)60= 36 333,9 Euro. Ce qui donne un montant d'intérêt de 16 333,9 Euro (36 333,9-20 000)
- Offre de la banque B :
20 000(1+0,03)3x5 = 31 159,3 Euro. C'est à dire un montant d'intérêt de 11 159,3 Euro
L'offre de la banque B donnerait moins d'intérêt à payer que l'offre de la banque A donc on préfère toujours un taux d'intérêt trimestriel de 3% qu'un taux mensuel de 1%.
4. Un couple vient d'avoir un bébé et ils se demandent comment ils peuvent lui offrir une meilleure éducation universitaire dans 18 ans plus tard. Pour cela il veulent savoir combien il faut placer annuellement, dès aujourd'hui, jusqu'à la 17ème anniversaire de leur fils pour avoir en retour, au bout de l'age de 18 ans et pendant quatre ans, quatre annuités de 20 000 Euro qui vont servir au financement de ses études universitaires.
La banque propose un TAEG de 10%.
Pour résoudre un tel problème, on peut toujours procéder de différentes façons et arriver nécessairement au même résultat. L'essentiel dans toutes ses solutions consiste à chercher un inconnu (le montant à placer annuellement dans cet exercice) en comparant des montants ramenés à une date précise dans le temps (toute comparaison en finance doit se faire à une même date en y capitalisant et actualisant des sommes dispersées dans le temps).
 En regardant le schéma, la question à poser est de dire que les différents montants à placer doivent être équivalents, financièrement parlant, aux mêmes montants que je vais recevoir de la banque dans 18 ans pendant 4 ans. Cette question nous donne bien l'équation à formuler pour trouver l'inconnu a mais il reste à choisir une date de comparaison (on peut choisir n'importe quelle date, la solution sera la même).
En regardant le schéma, la question à poser est de dire que les différents montants à placer doivent être équivalents, financièrement parlant, aux mêmes montants que je vais recevoir de la banque dans 18 ans pendant 4 ans. Cette question nous donne bien l'équation à formuler pour trouver l'inconnu a mais il reste à choisir une date de comparaison (on peut choisir n'importe quelle date, la solution sera la même).Je vais choisir spontanément la date 0. Donc, on actualise les différents placements a à la date 0 pour obtenir une valeur actuelle des différents placements qui doit égaliser la valeur actuelle à la date 0 des différents montants à recevoir à partir de l'age de 18 ans.

D'où on a 9,20 a = 12 542,82 ==> a = 1 363,4 Euro, c'est à dire approximativement une moyenne de 114 Euro mensuellement.
5. L'utilisation de rachat ou regroupement de crédit dans la situation ou on est confronté à une série de mensualités de différents emprunts contractés pour financer des projets différents, est la meilleurs solution proposée par les banques jusqu'à présent. Pour en savoir plus cliquez sur la notion de rachat de crédit. Accédez aux liens ci-avant pour des exemples pratiques.
A suivre ...
Réaction aux commentaires :
Merci Laetitia pour votre commentaire. Effectivement j'ai eu une confusion en pensant au nombre de trimestres dans l'année au lieu du nombre de mois dans le trimestre.
Pour info utile :
Un semestre est une période de 6 mois [Le mot semestre vient du latin sex(six) et mentis(mois)] source : Wiktionnaire

Un quadrimestre est une période de 4 mois, une année se compose donc de 3 quadrimestres.
 Un trimestre est un espace de trois mois, il Y en a 4 sur l'année.
Un trimestre est un espace de trois mois, il Y en a 4 sur l'année.
Inscription à :
Articles (Atom)
Calculs financiers - ComptabilitéPour partir sur de bonnes bases : une série d'exercices résolus de la comptabilité générale de sorte à faire comprendre la logique et la technique de la partie double sur laquelle les écritures comptables se basent.
EmpruntApprendre à résoudre des problèmes réels liés à l'emprunt par l'utilisation de quelques formules de mathématiques financières :
- MensualitéLe remboursement d'un crédit se fait par des montants fractionnés (mensualités, annuités ...) et étalés dans le temps. Ces montants sont calculés de façon différente selon le type du remboursement :
- Rachat de créditsDes exemples pratiques de rachat de crédits pour mieux comprendre l'opportunité ou les avantages et inconvénients d'une telle solution financière pour les emprunteurs en difficulté de paiement. - FRAIllustrations des techniques utilisées par les banques pour proposer à leurs clients une offre de couverture du risque :
- Autres calculsD'autres calculs de la gestion financière :
TEG - Actualisation - VAN - TIR - Cash Flow ...
EmpruntApprendre à résoudre des problèmes réels liés à l'emprunt par l'utilisation de quelques formules de mathématiques financières :
- L'importance des mathématiques financières
- Calculer un emprunt : formules de base
- Emprunt immobilier : tableau d'amortissement financier
- Emprunt bancaire : problèmes et solutions
- MensualitéLe remboursement d'un crédit se fait par des montants fractionnés (mensualités, annuités ...) et étalés dans le temps. Ces montants sont calculés de façon différente selon le type du remboursement :
- Comment calcule-t-on les mensualités d'un emprunt ?
- Annuité constante
- Remboursement constant du capital
- Taux de chargement : mensualité constante et remboursement constant du capital
- Rachat de créditsDes exemples pratiques de rachat de crédits pour mieux comprendre l'opportunité ou les avantages et inconvénients d'une telle solution financière pour les emprunteurs en difficulté de paiement. - FRAIllustrations des techniques utilisées par les banques pour proposer à leurs clients une offre de couverture du risque :
- FRA (Forward Rate Agreement) : couverture sur taux d'intérêt
- Couverture du risque d'une évolution défavorable du cours de change
- Autres calculsD'autres calculs de la gestion financière :
TEG - Actualisation - VAN - TIR - Cash Flow ...
Ces articles peuvent aussi vous intéresser
____________________________Calcul de la mensualité d'emprunt
De plus en plus de personnes font recours à l'emprunt pour financer leurs projets les plus coûteux. Pourtant, peu d'entre eux sachent comment calculer la ou les mensualités d'un emprunt. C'est dans ce blog que vous trouverez les différentes méthodes de calcul en la matière._____________________________
Rachat de crédit
Le rachat de crédit se présente comme une solution efficace au problème de surendettement. Il consiste à substituer le crédit ou les différents crédits en un seul plus avantageux quant à la charge de mensualité à rembourser. Dans ce blog, vous trouverez des explications avec illustrations par des exemples pratiques sur le fonctionnement de la technique de rachat de crédit._____________________________
Plus sur l'annuaire de cours gratuits
 Cours de Finance
Cours de FinanceLes cours ayant une relation avec la gestion de l'argent.
Sous catégories: Banque | Assurance | Bourse
 Cours de mathématiques
Cours de mathématiquesTout cours de mathématique sous toute ses branches.
Sous catégories: Maths financières | Probabilité/statistique
 Cours d'économie
Cours d'économieLes cours ayant un rapport avec l'économie en générale et particulièrement la macro et micro économie.
Sous catégories: Macro-économie | Micro-économie

Vs semblez bien nager dans ces calculs et pas aussi versé pourriez vs me donner la méthode pour calculer simplement :
...le montant total acquis aprés "x ans" si je place --cumulativement -
par ex: 1 €...tous les mois... ou tous les 3 mois... à un Taux "T% annuel" SVP ? Car je m'y perds ! Doit-on utiliser la Valeur Actuelle ?
Merci pour l'aide Potentielle ! PjsA (mon e-mail=> "pjsa@voila.fr")