Calculer un emprunt : formules de base

Dans cette partie du blog, j'essaierai de simplifier la compréhension des mathématiques financières appliquées au différents calculs d'un emprunt ou d'un prêt. Je ne vais pas démontrer les formules que je vous expliquerai ici mais je me concentrerai plus sur leur signification et leur utilité dans la pratique de tous les jours pour éviter que cela ne soit un cours mathématique abstrait privé de tout sens pratique ou presque.

Dans les formules suivantes, vous avez l'essentiel des mathématiques financières, vous pouvez en déduire toutes les autres formules avec quelques simples touches mathématiques.

Valeur actuelle Vo d’une valeur future Vn actualisée sur n périodes à un taux i

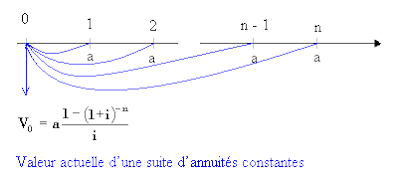Valeur acquise Vn par un capital Vo placé pendant n périodes à un taux i



Actualisation / Capitalisation :



La première formule représente la valeur actuelle V0 (actualisation) d'une valeur future Vn actualisée sur n périodes à un taux i. De cette formule on en déduit la valeur future ou acquise Vn (capitalisation) en fonction du capital V0 placé pendant n périodes à un taux i.


Quelques exemple pratiques de ces formules :

1. Combien dois-je placer aujourd'hui au taux de 8% pour avoir 10 000 Euro dans 3 ans ?


2. Je veux acheter dans 5 ans une voiture au prix de 50 000 Euro, la banque me propose un taux d'intérêt de 12%. Combien dois-je placer mensuellement pour que je puisse disposer de ce montant exact dans 5 ans ?

Pour mieux répondre à cette question, il faut savoir traduire correctement ces données sur une ligne de temps et reposer la même question mais sous forme de schéma.

Avec Vn= 50 000 Euro et n = 60

Donc la question reformulée dans ce schéma est de savoir combien je dois placer mensuellement dès aujourd'hui pour que j'aie, grâce au produits de ces placements, au bout de la cinquième année, c'est à dire dans 60 mois, un montant de 50 000 Euro ?

Il faut bien savoir que le taux proposé par la banque est un taux annuel qu'il faut convertir au taux mensuel. Pour cela il faut distinguer entre un taux proportionnel et un taux équivalent.

Taux mensuel proportionnel = taux annuel /12 mois (les banques l'utilise incorrectement car ce taux équivaut au taux d'intérêts simples mais pas composés. En effet, le placement d'un Euro en intérêt simple mensuellement au taux i donnera à la fin de l'année un montant d'intérêt de 12i. De l'autre côté, le produit en intérêt de ce même placement pendant un an au taux annuel r donnerait un montant d'intérêt égal r. Donc, en supposant l'équivalence de ces deux montants d'intérêt nous obtiendront la formule du taux proportionnel )

Taux équivalent : c'est en fait le taux mensuel qui donnerait le même résultat que le taux annuel dans le cas d'un placement d'un même montant.

Juste à titre d'information, au niveau des emprunts bancaires et surtout les emprunts immobiliers, on utilise le taux proportionnel et pas celui équivalent ce qui profite le plus aux banques puisque le taux proportionnel (1/12=1% dans notre exemple) est toujours plus grand que celui équivalent (0,95% dans notre cas) qui reflète le vrai taux mensuel correspondant au taux annuel proposé par la banque.

Revenons à notre exemple, Il suffit donc de remplacer dans la formule Vn les valeurs suivantes : t=0,95%, n=60 et Vn= 50 000 pour trouver le montant a qu'il faut placer mensuellement pendant 5 ans.

Donc si je place chaque mois un montant de 622,12 Euro au taux annuel de 12% j'aurais au bout de la cinquième année 50 000 Euro à raison de 37 327,2 Euro (= 622,12 x 60) remboursement des mensualités placées et le reste 12 672,8 Euro comme intérêts sur les placements.

Plus de cas pratiques de calcul d'emprunts plus loin.

Réaction aux commentaires :

_____________________
Pour répondre à votre question, on applique la formule de la valeur acquise cité ci-dessous comme illustré sur l'image suivante :
Cette formule nous donne bien ce que j'aurais à la fin de la Xième année d'un placement de 1€ mensuellement au taux annuelle T%.

Si je place 1€ chaque 3mois, je remplacerais T%/12 par T%/4 et 12.X par 4.X.

Emprunt immobilier : tableau d'amortissement financier

Un tableau d'amortissement des emprunts ou d'amortissement financier c'est un plan de remboursement d'un emprunt par le moyen de décaissements échelonnés. Il permet de mettre en évidence, à toutes les échéances, la part de l'emprunt remboursé, l'emprunt restant à rembourser, le montant de l'intérêt et la mensualité (intérêt+ emprunt remboursé). Ces quatre éléments sont primordiaux pour toute comparaison d'offre et la prise d'une meilleure décision.

Je mets à votre disposition : un tableau de calcul automatique des emprunts. Il vous permet de comparer facilement les différents offres sur le marché et de visualiser les différents éléments qui vous permettent de prendre votre décision d'emprunt.

Comment peut-on s'en servir ?

Je vous mets un exemple ci-dessous d'un emprunt de 5000 Euro au taux annuel de 12% à rembourser par 14 paiements mensuels. Une fois ces données introduites vous n'avez qu'à cliquer pour obtenir le tableau d'amortissement.


Dans le tableau vous aurez quatre colonnes principales que je vous explique ci-dessous en donnant comme exemple les calculs de la première ligne :

• Montant paiement : c'est la mensualité à payer = montant intérêt + part du capital à rembourser (principal). Pour la calculer, on a besoin d'une autre formule car la part du capital est inconnue pour le moment, donc pour la calculer nous avons une autre formule : Cette formule est celle appliquée au niveau des emprunts immobiliers, pourtant elle n'est pas la seul méthode de calcul de la mensualité
  
• Montant intérêt : c'est la part d'intérêt = Restant à payer x taux mensuel proportionnel = 5000 x 12%/12 = 50
  
• Principal : La part du capital à rembourser = mensualité - montant intérêt = 384,51 - 50 = 334,51
  
• Restant à payer : C'est ce qui reste à payer en déduisant les parts du capital déjà payées = 5000 - 334,51 = 4665,49

Réaction aux commentaires :

marie a dit…

bonjour sur votre exemple, pouvez-vous me dire à quoi correspond le chiffre 1 dans votre formule de calcul de la mensualité et peut-on faire cette formule sur une calculatrice;

merci

----------------

Le 1 dans la formule cité ici vient de la formule de la valeur actuelle d'une suite d'annuités (ou mensualités) qui devrait être égale au capital emprunté.

Si vous remplacez V0 par K, a par m et i par t/12 vous arrivez à la même formule cité dans cette article, qui provient de l'actualisation de chaque montant "a" à la période 0.

Pour le calculer dans une calculatrice, oui c'est possible et il faut apprendre à le faire en une seule fois pour arriver au résultat le plus juste possible.

j'espère que cela répond à votre question.

Emprunt bancaire : problèmes et solutions

Dans cette partie du blog, vous allez vous familiariser avec l'utilisation des formules mathématiques à la résolution de problèmes pratiques liés à la finance.

J'apprécierai tout problème ou question postée dans les commentaires, je m'efforcerai de lui apporter une bonne réponse. Alors n'hésitez pas.

3. Je veux emprunter 20 000 Euro à rembourser sur 5 ans pour financer un projet d'investissement. Pour cela, j'ai reçu deux offres de deux banques différentes :

• Banque A : 1% (taux mensuel), remboursements mensuels
  
• Banque B : 3% par trimestre (taux trimestriel)

Quelle proposition faut-t-il choisir ?

Il faut noter qu'il n'y a pas qu'une solution possible pour des problèmes à résoudre au moyen des mathématiques financières.

Première solution :

On peut comparer les taux des deux banques. Mais attention, il faut comparer des choses comparables. Dans ce cas, les taux sont pour des périodes différentes. Pour cela, il faut calculer le taux équivalent de l'un par rapport à l'autre. C'est à dire, comparer, par exemple, au taux mensuel de 1%, le taux mensuel équivalent (à trouver) au taux de 3% (trimestriel)

Pour facilité la formulation du problème, on se demande, quelle est le taux d'intérêt mensuel i (inconnu) qui donnerais le même résultat que le taux trimestriel de 3% pour le placement d'un montant identique M pendant 3 mois (1 trimestre).

• Le placement d'un montant M au taux mensuel i pendant 3 mois : Mx(1+i)⁴

• Le placement d'un montant M au taux trimestriel de 3% pendant 1 trimestre : Mx(1+3%)

Donc pour supposer l'équivalence entre les deux résultats on a : Mx(1+i)⁴ = Mx(1+3%) c'est à dire que i = (1+3%)^1/4 - 1 = 0,74% c'est ce taux mensuel équivalent au taux trimestriel de 3% qu'il faut comparer avec le Taux mensuel de 1% proposé par la banque A.

Donc vous voyez bien que la proposition de la banque B (0,74% mensuel) est moins coûteuse donc meilleure que celle de A (1% mensuel).

Deuxième solution :

On pourrait résoudre ce problème de la même façon mais en comparant, cette fois ci, le taux trimestriel de 3% avec le taux trimestriel équivalent au taux mensuel de 1%.

Le placement d'un montant M au taux de 1% mensuel pendant 3 mois : Mx(1+1%)⁴

Le placement du même montant M au taux t trimestriel pendant un trimestre (4mois) : Mx(1+t)

L'équivalence entre les deux taux d'intérêt donnerait le même résultat : Mx(1+1%)⁴ = Mx(1+t)

C'est à dire t = (1+1%)⁴ - 1 = 4,06 %

Donc vous voyez que vous arrivez au même résultat. Que vous utilisez la première solution ou la deuxième la proposition de la banque B reste la meilleure.

Troisième solution :

On pourrait résoudre ce problème en comparant tout simplement le montant d'intérêt de chacune des propositions et choisir la solution qui donnerait moins d'intérêts à payer. Pour cela, on calcule la capitalisation de 20 000 Euro pendant 5 ans pour les deux propositions.

• Offre de la banque A :

La banque A nous propose des mensualités à 1% pendant 5 ans c'est à dire pendant 5x12= 60 mois

20 000(1+0,01)⁶⁰= 36 333,9 Euro. Ce qui donne un montant d'intérêt de 16 333,9 Euro (36 333,9-20 000)

• Offre de la banque B :

20 000(1+0,03)^3x5 = 31 159,3 Euro. C'est à dire un montant d'intérêt de 11 159,3 Euro

L'offre de la banque B donnerait moins d'intérêt à payer que l'offre de la banque A donc on préfère toujours un taux d'intérêt trimestriel de 3% qu'un taux mensuel de 1%.

4. Un couple vient d'avoir un bébé et ils se demandent comment ils peuvent lui offrir une meilleure éducation universitaire dans 18 ans plus tard. Pour cela il veulent savoir combien il faut placer annuellement, dès aujourd'hui, jusqu'à la 17^ème anniversaire de leur fils pour avoir en retour, au bout de l'age de 18 ans et pendant quatre ans, quatre annuités de 20 000 Euro qui vont servir au financement de ses études universitaires.

La banque propose un TAEG de 10%.

Pour résoudre un tel problème, on peut toujours procéder de différentes façons et arriver nécessairement au même résultat. L'essentiel dans toutes ses solutions consiste à chercher un inconnu (le montant à placer annuellement dans cet exercice) en comparant des montants ramenés à une date précise dans le temps (toute comparaison en finance doit se faire à une même date en y capitalisant et actualisant des sommes dispersées dans le temps).

En regardant le schéma, la question à poser est de dire que les différents montants à placer doivent être équivalents, financièrement parlant, aux mêmes montants que je vais recevoir de la banque dans 18 ans pendant 4 ans. Cette question nous donne bien l'équation à formuler pour trouver l'inconnu a mais il reste à choisir une date de comparaison (on peut choisir n'importe quelle date, la solution sera la même).

Je vais choisir spontanément la date 0. Donc, on actualise les différents placements a à la date 0 pour obtenir une valeur actuelle des différents placements qui doit égaliser la valeur actuelle à la date 0 des différents montants à recevoir à partir de l'age de 18 ans.


D'où on a 9,20 a = 12 542,82 ==> a = 1 363,4 Euro, c'est à dire approximativement une moyenne de 114 Euro mensuellement.

5. L'utilisation de rachat ou regroupement de crédit dans la situation ou on est confronté à une série de mensualités de différents emprunts contractés pour financer des projets différents, est la meilleurs solution proposée par les banques jusqu'à présent. Pour en savoir plus cliquez sur la notion de rachat de crédit. Accédez aux liens ci-avant pour des exemples pratiques.

A suivre ...

Réaction aux commentaires :

Merci Laetitia pour votre commentaire. Effectivement j'ai eu une confusion en pensant au nombre de trimestres dans l'année au lieu du nombre de mois dans le trimestre.

Pour info utile :

Un semestre est une période de 6 mois [Le mot semestre vient du latin sex(six) et mentis(mois)] source : Wiktionnaire


Un quadrimestre est une période de 4 mois, une année se compose donc de 3 quadrimestres. Un trimestre est un espace de trois mois, il Y en a 4 sur l'année.